Preface ....................................................... xix
PART I. VECTOR AND TENSOR ALGEBRA ............................... 1
1 Vector Algebra ............................................... 3
1.1 Inner Product. Cross Product ............................ 3
1.2 Cartesian Coordinate Frames ............................. 6
1.3 Summation Convention. Components of a Vector and
a Point ................................................. 6
2 Tensor Algebra ............................................... 9
2.1 What Is a Tensor? ....................................... 9
2.2 Zero and Identity Tensors. Tensor Product of Two
Vectors. Projection Tensor. Spherical Tensor ........... 10
2.3 Components of a Tensor ................................. 11
2.4 Transpose of & Tensor. Symmetric and Skew Tensors ...... 12
2.5 Product of Tensors ..................................... 13
2.6 Vector Cross. Axial Vector of a Skew Tensor ............ 15
2.7 Trace of a Tensor. Deviatoric Tensors .................. 16
2.8 Inner Product of Tensors. Magnitude of a Tensor ........ 17
2.9 Invertible Tensors ..................................... 19
2.10 Determinant of a Tensor ................................ 21
2.11 Cofactor of a Tensor ................................... 22
2.12 Qrthogonal Tensors ..................................... 25
2.13 Matrix of a Tensor ..................................... 26
2.14 Eigenvalues and Eigenvectors of a Tensor. Spectral
Theorem ................................................ 28
2.15 Square Root of a Symmetric, Positive-Definite Tensor.
Polar Decomposition Theorem ............................ 31
2.16 Principal Invariants of a Tensor. Cayley-Hamilton
Equation ............................................... 35
PART II. VECTOR AND TENSOR ANALYSIS ............................ 39
3 Differentiation ............................................. 41
3.1 Differentiation of Functions of a Scalar ............... 41
3.2 Differentiation of Fields. Gradient .................... 43
3.3 Divergence and Curl. Vector and Tensor Identities ...... 46
3.4 Differentiation of a Scalar Function of a Tensor ....... 49
4 Integral Theorems ........................................... 52
4.1 The Divergence Theorem ................................. 52
4.2 Line Integrals. Stokes' Theorem ........................ 53
PART III. KINEMATICS ........................................... 59
5 Motion of a Body ............................................ 61
5.1 Reference Body. Material Points ........................ 61
5.2 Basic Quantities Associated with the Motion of a Body .. 61
5.3 Convection of Sets with the Body ....................... 63
6 The Deformation Gradient .................................... 64
6.1 Approximation of a Deformation by a Homogeneous
Deformation ............................................ 64
6.1.1 Homogeneous Deformations ........................ 64
6.1.2 General Deformations ............................ 65
6.2 Convection of Geometric Quantities ..................... 66
6.2.1 Infinitesimal Fibers ............................ 66
6.2.2 Curves .......................................... 67
6.2.3 Tangent Vectors ................................. 67
6.2.4 Bases ........................................... 68
7 Stretch, Strain, and Rotation ............................... 69
7.1 Stretch and Rotation Tensors. Strain ................... 69
7.2 Fibers. Properties of the Tensors U and С .............. 70
7.2.1 Infinitesimal Fibers ............................ 70
7.2.2 Finite Fibers ................................... 71
7.3 Principal Stretches and Principal Directions ........... 73
8 Deformation of Volume and Area .............................. 75
8.1 Deformation of Normals ................................. 75
8.2 Deformation of Volume .................................. 76
8.3 Deformation of Area .................................... 77
9 Material and Spatial Descriptions of Fields ................. 80
9.1 Gradient, Divergence, and Curl ......................... 80
9.2 Material and Spatial Time Derivatives .................. 81
9.3 Velocity Gradient ...................................... 82
9.4 'Commutator Identities ................................. 84
9.5 Particle Paths ......................................... 85
9.6 Stretching of Deformed Fibers .......................... 85
10 Special Motions ............................................. 86
10.1 Rigid Motions .......................................... 86
10.2 Motions Whose Velocity Gradient is Symmetric and
Spatially Constant ..................................... 87
11 Stretching and Spin in an Arbitrary Motion .................. 89
11.1 Stretching and Spin as Tensor Fields ................... 89
11.2 Properties of D ........................................ 90
11.3 Stretching and Spin Using the Current Configuration
as Reference ........................................... 92
12 Material and Spatial Tensor Fields. Pullback and
Pushforward Operations ...................................... 95
12.1 Material and Spatial Tensor Fields ..................... 95
12.2 Pullback and Pushforward Operations .................... 95
13 Modes of Evolution for Vector and Tensor Fields ............. 98
13.1 Vector and Tensor Fields That Convect With the Body .... 98
13.1.1 Vector Fields That Convect as Tangents .......... 98
13.1.2 Vector Fields That Convect as Normals ........... 99
13.1.3 Tangentially Convecting Basis and Its Dual
Basis. Covariant and Contravariant Components
of Spatial Fields ............................... 99
13.1.4 Covariant and Contravariant Convection of
Tensor Fields .................................. 102
13.2 Corotational Vector and Tensor Fields ................. 105
14 Motions with Constant Velocity Gradient .................... 107
14.1 Motions ............................................... 107
15 Material and Spatial Integration ........................... 109
15.1 Line Integrals ........................................ 109
15.2 Volume and Surface Integrals .......................... 109
15.2.1 Volume Integrals ............................... 110
15.2.2 Surface Integrals .............................. 111
15.3 Localization of Integrals ............................. 111
16 Reynolds' Transport Relation. Isochoric Motions ......... 113
17 More Kinematics ............................................ 115
17.1 Vorticity ............................................. 115
17.2 Transport Relations for Spin and Vorticity ............ 115
17.3 Irrotational Motions .................................. 117
17.4 Circulation ........................................... 118
17.5 Vortex Lines .......................................... 120
17.6 Steady Motions ........................................ 121
17.7 A Class of Natural Reference Configurations for
Fluids ................................................ 122
17.8 The Motion Problem .................................... 122
17.8.1 Kinematical Boundary Conditions ................ 122
17.8.2 The Motion Problem in a Fixed Container ........ 123
17.8.3 The Motion Problem in All of Space. Solution
with Constant Velocity Gradient ................ 123
PART IV. BASIC MECHANICAL PRINCIPLES .......................... 125
18 Balance of Mass ............................................ 127
18.1 Global Form of Balance of Mass ........................ 127
18.2 Local Forms of Balance of Mass ........................ 128
18.3 Simple Consequences of Mass Balance ................... 129
19 Forces and Moments. Balance Laws for Linear and Angular
Momentum ................................................... 131
19.1 Inertial Frames. Linear and Angular Momentum .......... 131
19.2 Surface Tractions. Body Forces ........................ 132
19.3 Balance Laws for Linear and Angular Momentum .......... 134
19.4 Balance of Forces and Moments Based on the
Generalized Body Force ................................ 136
19.5 Cauchy's Theorem for the Existence of Stress .......... 137
19.6 Local Forms of the Force and Moment Balances .......... 139
19.7 Kinetic Energy. Conventional and Generalized External
Power Expenditures .................................... 141
19.7.1 Conventional Form of the External Power ........ 142
19.7.2 Kinetic Energy and Inertial Power .............. 142
19.7.3 Generalized Power Balance ...................... 143
19.7.4 The Assumption of Negligible Inertial Forces ... 144
20 Frames of Reference ........................................ 146
20.1 Changes of Frame ...................................... 146
20.2 Frame-Indifferent Fields .............................. 147
20.3 Transformation Rules for Kinematic Fields ............. 148
20.3.1 Material Time-Derivatives of Frame-
Indifferent Tensor Fields are Not Frame-
Indifferent .................................... 151
20.3.2 The Corotational, Covariant, and
Contravariant Rates of a Tensor Field .......... 151
20.3.3 Other Relations for the Corotational Rate ...... 152
20.3.4 Other Relations for the Covariant Rate ......... 153
20.3.5 Other Relations for the Contravariant Rate ..... 154
20.3.6 General Tensorial Rate ......................... 155
21 Frame-Indifference Principle ............................... 157
21.1 Transformation Rules for Stress and Body Force ........ 157
21.2 Inertial Body Force in a Frame That Is Not Inertial ... 159
22 Alternative Formulations of the Force and Moment Balances .. 161
22.1 Force and Moment Balances as a Consequence of
Frame-Indifference of the Expended Power .............. 161
22.2 Principle of Virtual Power ............................ 163
22.2.1 Application to Boundary-Value Problems ......... 165
22.2.2 Fundamental Lemma of the Calculus of
Variations ..................................... 167
23 Mechanical Laws for a Spatial Control Volume ............... 168
23.1 Mass Balance for a Control Volume .....................
23.2 Momentum Balances for a Control Volume ................ 169
24 Referential Forms for the Mechanical Laws .................. 173
24.1 Piola Stress. Force and Moment Balances ............... 173
24.2 Expended Power ........................................ 175
25 Further Discussion of Stress ............................... 177
25.1 Power-Conjugate Pairings. Second Piola Stress ......... 177
25.2 Transformation Laws for the Piola Stresses ............ 178
PART V. BASIC THERMODYNAMICAL PRINCIPLES ...................... 181
26 The First Law: Balance of Energy ........................... 183
26.1 Global and Local Forms of Energy Balance .............. 184
26.2 Terminology for "Extensive" Quantities ................ 185
27 The Second Law: Nonnegative Production of Entropy .......... 186
27.1 Global Form of the Entropy Imbalance .................. 187
27.2 Temperature and the Entropy Imbalance ................. 187
27.3 Free-Energy Imbalance. Dissipation .................... 188
28 General Theorems ........................................... 190
28.1 Invariant Nature of the First Two Laws ................ 190
28.2 Decay Inequalities for the Body Under Passive
Boundary Conditions ................................... 191
28.2.1 Isolated Body .................................. 191
28.2.2 Boundary Essentially at Constant Pressure and
Temperature .................................... 192
29 A Free-Energy Imbalance for Mechanical Theories ............ 194
29.1 Free-Energy Imbalance. Dissipation .................... 194
29.2 Digression: Role of the Free-Energy Imbalance within
the General Thermodynamic Framework ................... 195
29.3 Decay Inequalities .................................... 196
30 The First Two Laws for a Spatial Control Volume ............ 197
31 The First Two Laws Expressed Referentially ................. 199
31.1 Global Forms of the First Two Laws .................... 200
31.2 Local Forms of the First Two Laws ..................... 201
31.3 Decay Inequalities for the Body Under Passive
Boundary Conditions ................................... 202
31.4 Mechanical Theory: Free-Energy Imbalance .............. 204
PART VI. MECHANICAL AND THERM OD YNAMICAL LAWS AT A SHOCK
WAVE .......................................................... 207
32 Shock Wave Kinematics ...................................... 209
32.1 Notation. Terminology ................................. 209
32.2 Hadamard's Compatibility Conditions ................... 210
32.3 Relation Between the Scalar Normal Velocities VR and
V ..................................................... 212
32.4 Transport Relations in the Presence of a Shock Wave ... 212
32.5 The Divergence Theorem in the Presence of a Shock
Wave .................................................. 215
33 Basic Laws at a Shock Wave: Jump Conditions ................ 216
33.1 Balance of Mass and Momentum .......................... 216
33.2 Balance of Energy and the Entropy Imbalance ........... 218
PART VII. INTERLUDE: BASIC HYPOTHESES FOR DEVELOPING
PHYSICALLY MEANINGFUL CONSTITUTIVE THEORIES ................... 221
34 General Considerations ..................................... 223
35 Constitutive Response Functions ............................ 224
36 Frame-Indifference and Compatibility with Thermodynamics ... 225
PART VIII. RIGID HEAT CONDUCTORS .............................. 227
37 Basic Laws ................................................. 229
38 General Constitutive Equations ............................. 230
39 Thermodynamics and Constitutive Restrictions: The
Coleman-Noll Procedure ..................................... 232
40 Consequences of the State Restrictions ..................... 234
41 Consequences of the Heat-Conduction Inequality ............. 236
42 Fourier's Law .............................................. 237
PART IX. THE MECHANICAL THEORY OF COMPRESSIBLE AND
INCOMPRESSIBLE FLUIDS ......................................... 239
43 Brief Review ............................................... 241
43.1 Basic Kinematical Relations ........................... 241
43.2 Basic Laws ............................................ 241
43.3 Transformation Rules and Objective Rates .............. 242
44 Elastic Fluids ............................................. 244
44.1 Constitutive Theory ................................... 244
44.2 Consequences of Frame-Indifference .................... 244
44.3 Consequences of Thermodynamics ........................ 245
44.4 Evolution Equations ................................... 246
45 Compressible, Viscous Fluids ............................... 250
45.1 General Constitutive Equations ........................ 250
45.2 Consequences of Frame-Indifference .................... 251
45.3 Consequences of Thermodynamics ........................ 253
45.4 Compressible, Linearly Viscous Fluids ................. 255
45.5 Compressible Navier-Stokes Equations .................. 256
45.6 Vorticity Transport Equation .......................... 256
46 Incompressible Fluids ...................................... 259
46.1 Free-Energy Imbalance for an Incompressible Body ...... 259
46.2 Incompressible, Viscous Fluids ........................ 260
46.3 Incompressible, Linearly Viscous Fluids ............... 261
46.4 Incompressible Navier-Stokes Equations ................ 262
46.5 Circulation. Vorticity-Transport Equation ............. 263
46.6 Pressure Poisson Equation ............................. 265
46.7 Transport Equations for the Velocity Gradient,
Stretching, and Spin in a Linearly Viscous,
Incompressible Fluid .................................. 265
46.8 Impetus-Gauge Formulation of the Navier-Stokes
Equations ............................................. 267
46.9 Perfect Fluids ........................................ 268
PART X. MECHANICAL THEORY OF ELASTIC SOLIDS ................... 271
47 Brief Review ............................................... 273
47.1 Kinematical Relations ................................. 273
47.2 Basic Laws ............................................ 273
47.3 Transformation Laws Under a Change in Frame ........... 274
48 Constitutive Theory ........................................ 276
48.1 Consequences of Frame-Indifference .................... 276
48.2 Thermodynamic Restrictions ............................ 278
48.2.1 The Stress Relation ............................ 278
48.2.2 Consequences of the Stress Relation ............ 280
48.2.3 Natural Reference Configuration ................ 280
49 Summary of Basic Equations. Initial/Boundary-Value
Problems ................................................... 282
49.1 Basic Field Equations ................................. 282
49.2 A Typical Initial/Boundary-Value Problem .............. 283
50 Material Symmetry .......................................... 284
50.1 The Notion of a Group. Invariance Under a Group ....... 284
50.2 The Symmetry Group Q .................................. 285
50.2.1 Proof That Q Is a Group ........................ 288
50.3 Isotropy .............................................. 288
50.3.1 Free Energy Expressed in Terms of Invariants ... 290
50.3.2 Free Energy Expressed in Terms of Principal
stretches ...................................... 292
51 Simple Shear of a Homogeneous, Isotropic Elastic Body ...... 294
52 The Linear Theory of Elasticity ............................ 297
52.1 Small Deformations .................................... 297
52.2 The Stress-Strain Law for Small Deformations .......... 298
52.2.1 The Elasticity Tensor .......................... 298
52.2.2 The Compliance Tensor .......................... 300
52.2.3 Estimates for the Stress and Free Energy ....... 300
52.3 Basic Equations of the Linear Theory of Elasticity .... 302
52.4 Special Forms for the Elasticity Tensor ............... 302
52.4.1 Isotropic Material ............................. 303
52.4.2 CubicCrystal ................................... 304
52.5 Basic Equations of the Linear theory of Elasticity
for an Isotropic Material ............................. 306
52.5.1 Statical Equations ............................. 307
52.6 Some Simple Statical Solutions ........................ 309
52.7 Boundary-Value Problems ............................... 310
52.7.1 Elastostatics .................................. 310
52.7.2 Elastodynamics ................................. 313
52.8 Sinusoidal Progressive Waves .......................... 313
53 Digression: Incompressibility .............................. 316
53.1 Kinematics of Incompressibility ....................... 316
53.2 Indeterminacy of the Pressure. Free-Energy Imbalance .. 317
53.3 Changes in Frame ...................................... 318
54 Incompressible Elastic Materials ........................... 319
54.1 Constitutive Theory ................................... 319
54.1.1 Consequences of Frame-Indifference ............. 319
54.1.2 Domain of Definition of the Response
Functions ...................................... 320
54.1.3 Thermodynamic Restrictions ..................... 321
54.2 Incompressible Isotropic Elastic Bodies ............... 323
54.3 Simple Shear of a Homogeneous, Isotropic,
Incompressible Elastic Body ........................... 324
55 Approximately Incompressible Elastic Materials ............. 326
PART XI. THERMOELASTICITY ..................................... 331
56 Brief Review ............................................... 333
56.1 Kinematical Relations ................................. 333
56.2 Basic Laws ............................................ 333
57 Constitutive Theory ........................................ 335
57.1 Consequences of Frame-Indifference .................... 335
57.2 Thermodynamic Restrictions ............................ 336
57.3 Consequences of the Thermodynamic Restrictions ........ 338
57.3.1 Consequences of the State Relations ............ 338
57.3.2 Consequences of the Heat-Conduction
Inequality ..................................... 339
57.4 Elasticity Tensor. Stress-Temperature Modulus. Heat
Capacity .............................................. 341
57.5 The Basic Thermoelastic Field Equations ............... 342
57.6 Entropy as Independent Variable. Nonconductors ........ 343
57.7 Nonconductors ......................................... 346
57.8 Material Symmetry ..................................... 346
58 Natural Reference Configuration for a Given Temperature .... 348
58.1 Asymptotic Stability and its Consequences. The
Gibbs Function ........................................ 348
58.2 Local Relations at a Reference Configuration that is
Natural for a Temperature ν0 .......................... 349
59 Linear Thermoelasticity .................................... 354
59.1 Approximate Constitutive Equations for the Stress
and Entropy ........................................... 354
59.2 Basic Field Equations of Linear Thermoelasticity ...... 356
59.3 Isotropic linear Thermoelasticity ..................... 356
PART XII. SPECIES DIFFUSION COUPLED TO ELASTICITY ............. 361
60 Balance Laws for Forces, Moments, and the Conventional
External Power ............................................. 363
61 Mass Balance for a Single Diffusing Species ................ 364
62 Free-Energy Imbalance Revisited. Chemical Potential ........ 366
63 Multiple Species ........................................... 369
63.1 Species Mass Balances ................................. 369
63.2 Free-Energy Imbalance ................................. 370
64 Digression: The Thermodynamic Laws in the Presence of
Species Transport .......................................... 371
65 Referential Laws ........................................... 374
65.1 Single Species ........................................ 374
65.2 Multiple Species ...................................... 376
66 Constitutive Theory for a Single Species ................... 377
66.1 Consequences of Frame-Indifference .................... 377
66.2 Thermodynamic Restrictions ............................ 378
66.3 Consequences of the Thermodynamic Restrictions ........ 380
66.4 Fick's Law ............................................ 382
67 Material Symmetry .......................................... 385
68 Natural Reference Configuration ............................ 388
69 Summary of Basic Equations for a Single Species ............ 390
70 Constitutive Theory for Multiple Species ................... 391
70.1 Consequences of Frame-Indifference and
Thermodynamics ........................................ 391
70.2 Fick's Law ............................................ 393
70.3 Natural Reference Configuration ....................... 393
71 Summary of Basic Equations for N Independent Species ....... 396
72 Substitutional Alloys ...................................... 398
72.1 Lattice Constraint .................................... 398
72.2 Substitutional Flux Constraint ........................ 399
72.3 Relative Chemical Potentials. Free-Energy Imbalance ... 399
72.4 Elimination of the Lattice Constraint. Larche-Cahn
Differentiation ....................................... 400
72.5 General Constitutive Equations ........................ 403
72.6 Thermodynamic Restrictions ............................ 404
72.7 Verification of (t) ................................... 406
72.8 Normalization Based on the Elimination of the
Lattice Constraint .................................... 406
73 Linearization .............................................. 408
73.1 Approximate Constitutive Equations for the Stress,
Chemical Potentials, and Fluxes ....................... 408
73.2 Basic Equations of the Linear Theory .................. 410
73.3 Isotropic Linear Theory ............................... 411
PART XIII. THEORY OF ISOTROPIC PLASTIC SOLIDS UNDERGOING
SMALL DEFORMATIONS ............................................ 415
74 Some Phenomenological Aspects of the Elastic-Plastic
Stress-Strain Response of Polycrystalline Metals ........... 417
74.1 Isotropic and Kinematic Strain-Hardening .............. 419
75 Formulation of the Conventional Theory. Preliminaries ... 422
75.1 Basic Equations ....................................... 422
75.2 Kinematical Assumptions that Define Plasticity
Theory ................................................ 423
75.3 Separability Hypothesis ............................... 424
75.4 Constitutive Characterization of Elastic Response ..... 424
76 Formulation of the Mises Theory of Plastic Flow ............ 426
76.1 General Constitutive Equations for Plastic Flow ....... 427
76.2 Rate-Independence ..................................... 428
76.3 Strict Dissipativity .................................. 430
76.4 Formulation of the Mises Flow Equations ............... 431
76.5 Initializing the Mises Flow Equations ................. 434
76.5.1 Flow Equations With Y(S) not Identically
Equal to S ..................................... 434
76.5.2 Theory with Flow Resistance as Hardening
Variable ....................................... 435
76.6 Solving the Hardening Equation. Accumulated Plastic
Strain is the Most General Hardening Variable ......... 435
76.7 Flow Resistance as Hardening Variable, Revisited ...... 439
76.8 Yield Surface. Yield Function. Consistency Condition .. 439
76.9 Hardening and Softening ............................... 443
77 Inversion of the Mises Flow Rule: W in Terms of Ё and T .... 445
78 Rate-Dependent Plastic Materials ........................... 449
78.1 Background ............................................ 449
78.2 Materials with Simple Rate-Dependence ................. 449
78.3 Power-Law Rate-Dependence ............................. 452
79 Maximum Dissipation ........................................ 454
79.1 Basic Definitions ..................................... 454
79.2 Warm-up: Derivation of the Mises Flow Equations
Based on Maximum Dissipation .......................... 456
79.3 More General Flow Rules. Drucker's Theorem ............ 458
79.3.1 Yield-Set Hypotheses ........................... 458
79.3.2 Digression: Some Definitions and Results
Concerning Convex Surfaces ..................... 460
79.3.3 Drucker's Theorem .............................. 461
79.4 The Conventional Theory of Perfectly Plastic
Materials v Fits within the Framework Presented Here .. 462
80 Hardening Characterized by a Defect Energy ................. 465
80.1 Free-Energy Imbalance Revisited ....................... 465
80.2 Constitutive Equations. Flow Rule ..................... 466
81 The Thermodynamics of Mises-Hill Plasticity ................ 469
81.1 Background ............................................ 469
81.2 Thermodynamics ........................................ 470
81.3 Constitutive Equations ................................ 470
81.4 Nature of the Defect Energy ........................... 472
81.5 The Flow Rule and the Boundedness Inequality .......... 473
81.6 Balance of Energy Revisited ........................... 473
81.7 Thermally Simple Materials ............................ 475
81.8 Determination of the Defect Energy by the Rosakis
Brothers, Hodowany, and Ravichandran .................. 476
81.9 Summary of the Basic Equations ........................ 477
82 Formulation of Initial/Boundary-Value Problems for the
Mises Flow Equations as Variational Inequalities ........... 479
82.1 Reformulation of the Mises Flow Equations in Terms
of Dissipation ........................................ 479
82.2 The Global Variational Inequality ..................... 482
82.3 Alternative Formulation of the Global Variational
Inequality When Hardening is Described by a Defect
Energy ................................................ 483
PART XIV. SMALL DEFORMATION, ISOTROPIC PLASTICITY BASED ON
THE PRINCIPLE OF VIRTUAL POWER ................................ 485
83 Introduction ............................................... 487
84 Conventional Theory Based on the Principle of Virtual
Power ...................................................... 489
84.1 General Principle of Virtual Power .................... 489
84.2 Principle of Virtual Power Based on the
Codirectionality Constraint ........................... 493
84.2.1 General Principle Based on Codirectionality .... 493
84.2.2 Streamlined Principle Based on
Codirectionality ............................... 495
84.3 Virtual External Forces Associated with Dislocation
Flow .................................................. 496
84.4 Free-Energy Imbalance ................................. 497
84.5 Discussion of the Virtual-Power Formulation ........... 498
85 Basic Constitutive Theory .................................. 499
86 Material Stability and Its Relation to Maximum
Dissipation ............................................. 501
PART XV. STRAIN GRADIENT PLASTICITY BASED ON THE PRINCIPLE
OF VIRTUAL POWER .............................................. 505
87 Introduction ............................................... 507
88 Kinematics ................................................. 509
88.1 Characterization of the Burgers Vector ................ 509
88.2 Irrotational Plastic Flow ............................. 511
89 The Gradient Theory of Aifantis ............................ 512
89.1 The Virtual-Power Principle of Fleck and Hutchinson ... 512
89.2 Free-Energy Imbalance ................................. 515
89.3 Constitutive Equations ................................ 516
89.4 Flow Rules ............................................ 517
89.5 Microscopically Simple Boundary Conditions ............ 518
89.6 Variational Formulation of the Flow Rule .............. 519
89.7 Plastic Free-Energy Balance ........................... 520
89.8 Spatial Oscillations. Shear Bands ..................... 521
89.8.1 Oscillations ................................... 521
89.8.2 Single Shear Bands and Periodic Arrays of
Shear Bands .................................... 521
90 The Gradient Theory of Gurtin and Anand .................... 524
90.1 Third-Order Tensors ................................... 524
90.2 Virtual-Power Formulation: Macroscopic and
Microscopic Force Balances ............................ 525
90.3 Free-Energy Imbalance ................................. 528
90.4 Energetic Constitutive Equations ...................... 528
90.5 Dissipative Constitutive Equations .................... 530
90.6 Flow Rule ............................................. 532
90.7 Microscopically Simple Boundary Conditions ............ 533
90.8 Variational Formulation of the Flow Rule .............. 534
90.9 Plastic Free-Energy Balance. Flow-Induced
Strengthening ......................................... 535
90.10 Rate-Independent Theory .............................. 536
PART XVI. LARGE-DEFORMATION THEORY OF ISOTROPIC PLASTIC
SOLIDS ........................................................ 539
91 Kinematics ................................................. 541
91.1 The Kröner Decomposition .............................. 541
91.2 Digression: Single Crystals ........................... 543
91.3 Elastic and Plastic Stretching and Spin. Plastic
Incompressibility ..................................... 543
91.4 Elastic and Plastic Polar Decompositions .............. 544
91.5 Change in Frame Revisited in View of the Kröner
Decomposition ......................................... 546
92 Virtual-Power Formulation of the Standard and Microscopic
Force Balances ............................................. 548
92.1 Internal and External Expenditures of Power ........... 548
92.2 Principle of Virtual Power ............................ 549
92.2.1 Consequences of Frame-Indifference ............. 550
92.2.2 Macroscopic Force Balance ...................... 551
92.2.3 Microscopic Force Balance ...................... 551
93 Free-Energy Imbalance ...................................... 553
93.1 Free-Energy Imbalance Expressed in Terms of the
Cauchy Stress ......................................... 553
94 Two New Stresses ........................................... 555
94.1 The Second Piola Elastic-Stress Te .................... 555
94.2 The Mandel Stress Me .................................. 556
95 Constitutive Theory ........................................ 557
95.1 General Separable Constitutive Theory ................. 557
95.2 Structural Frame-Indifference and the
Characterization of Polycrystalline Materials
Without Texture ....................................... 559
95.3 Interaction of Elasticity and Plastic Flow ............ 562
95.4 Consequences of Rate-Independence ..................... 563
95.5 Derivation of the Mises Flow Equations Based on
Maximum-Dissipation ................................... 564
96 Summary of the Basic Equations. Remarks .................... 566
97 Plastic Irrotationality: The Condition Wp = 0 .............. 567
98 Yield Surface. Yield Function. Consistency Condition ....... 569
99 |Dp| in Terms of Ė and Me .................................. 571
99.1 Some Important Identities ............................. 571
99.2 Conditions that Describe Loading and Unloading ........ 571
99.3 The Inverted Flow Rule ................................ 574
99.4 Equivalent Formulation of the Constitutive Equations
and Plastic Mises Flow Equations Based on the
Inverted Flow Rule .................................... 574
100 Evolution Equation for the Second Piola Stress ............ 576
101 Rate-Dependent Plastic Materials .......................... 579
101.1 Rate-Dependent Flow Rule ............................. 579
101.2 Inversion of the Rate-Dependent Flow Rule ............ 579
101.3 Summary of the Complete Constitutive Theory .......... 580
PART XVII. THEORY OF SINGLE CRYSTALS UNDERGOING SMALL
DEFORMATIONS .................................................. 583
102.1 Introduction ......................................... 583
102 Basic Single-Crystal Kinematics ........................... 586
103 The Burgers Vector and the Flow of Screw and Edge
Dislocations ............................................... 588
103.1 Decomposition of the Burgers Tensor G into
Distributions of Edge and Screw Dislocations ......... 588
103.2 Dislocation Balances ................................. 590
103.3 The Tangential Gradient 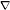 α on the Slip Plane Πα ...... 590
104 Conventional Theory of Single-Crystals .................... 593
104.1 Virtual-Power Formulation of the Standard and
Microscopic Force Balances ........................... 593
104.2 Free-Energy Imbalance ................................ 596
104.3 General Separable Constitutive Theory ................ 596
104.4 Linear Elastic Stress-Strain Law ..................... 597
104.5 Constitutive Equations for Flow with Simple Rate-
Dependence ........................................... 597
104.6 Power-Law Rate Dependence ............................ 601
104.7 Self-Hardening, Latent-Hardening ..................... 601
104.8 Summary of the Constitutive Theory ................... 602
105 Single-Crystal Plasticity at Small Length-Scales: A
Small-Deformation Gradient Theory .......................... 604
105.1 Virtual-Power Formulation of the Standard and
Microscopic Force Balances of the Gradient Theory .... 604
105.2 Free-Energy Imbalance ................................ 607
105.3 Energetic Constitutive Equations. Peach-Koehler
Forces ............................................... 607
105.4 Constitutive Equations that Account for Dissipation .. 609
105.5 Viscoplastic Flow Rule ............................... 612
105.6 Microscopically Simple Boundary Conditions ........... 615
105.7 Variational Formulation of the Flow Rule ............. 616
105.8 Plastic Free-Energy Balance .......................... 617
105.9 Some Remarks ......................................... 618
PART XVIII. SINGLE CRYSTALS UNDERGOING LARGE DEFORMATIONS ..... 621
106 Basic Single-Crystal Kinematics ........................... 623
107 The Burgers Vector and the Flow of Screw and Edge
Dislocations ............................................... 626
107.1 Transformation of Vector Area Measures Between the
Reference, Observed, and Lattice Spaces .............. 626
107.2 Characterization of the Burgers Vector ............... 627
107.3 The Plastically Convected Rate of G .................. 629
107.4 Densities of Screw and Edge Dislocations ............. 631
107.5 Comparison of Small- and Large-Deformation Results
Concerning Dislocation Densities ..................... 633
108 Virtual-Power Formulation of the Standard and Microscopic
Force Balances ............................................. 634
108.1 Internal and External Expenditures of Power .......... 634
108.2 Consequences of Frame-Indifference ................... 636
108.3 Macroscopic and Microscopic Force Balances ........... 637
109 Free-Energy Imbalance ..................................... 639
110 Conventional Theory ....................................... 641
110.1 Constitutive Relations ............................... 641
110.2 Simplified Constitutive Theory ....................... 643
110.3 Summary of Basic Equations ........................... 644
111 Taylor's Model of Polycrystal ............................. 646
111.1 Kinematics of a Taylor Polycrystal ................... 646
111.2 Principle of Virtual Power ........................... 648
111.3 Free-Energy Imbalance ................................ 651
111.4 Constitutive Relations ............................... 651
112 Single-Crystal Plasticity at Small Length Scales: A
Large-Deformation Gradient Theory .......................... 653
112.1 Energetic Constitutive Equations. Peach-Koehler
Forces ............................................... 653
112.2 Dissipative Constitutive Equations that Account for
Slip-Rate Gradients .................................. 654
l|2.3 Viscoplastic Flow Rule ............................... 656
112.4 Microscopically Simple Boundary Conditions ........... 657
112.5 Variational Formulation .............................. 658
112.6 Plastic Free-Energy Balance .......................... 659
112.7 Some Remarks ......................................... 660
113 Isotropic Functions ....................................... 665
113.1 Isotropic Scalar Functions ........................... 666
113.2 Isotropic Tensor Functions ........................... 666
113.3 Isotropic Linear Tensor Functions .................... 668
114 The Exponential of a Tensor ............................... 669
References ................................................. 671
Index ...................................................... 683 α on the Slip Plane Πα ...... 590
104 Conventional Theory of Single-Crystals .................... 593
104.1 Virtual-Power Formulation of the Standard and
Microscopic Force Balances ........................... 593
104.2 Free-Energy Imbalance ................................ 596
104.3 General Separable Constitutive Theory ................ 596
104.4 Linear Elastic Stress-Strain Law ..................... 597
104.5 Constitutive Equations for Flow with Simple Rate-
Dependence ........................................... 597
104.6 Power-Law Rate Dependence ............................ 601
104.7 Self-Hardening, Latent-Hardening ..................... 601
104.8 Summary of the Constitutive Theory ................... 602
105 Single-Crystal Plasticity at Small Length-Scales: A
Small-Deformation Gradient Theory .......................... 604
105.1 Virtual-Power Formulation of the Standard and
Microscopic Force Balances of the Gradient Theory .... 604
105.2 Free-Energy Imbalance ................................ 607
105.3 Energetic Constitutive Equations. Peach-Koehler
Forces ............................................... 607
105.4 Constitutive Equations that Account for Dissipation .. 609
105.5 Viscoplastic Flow Rule ............................... 612
105.6 Microscopically Simple Boundary Conditions ........... 615
105.7 Variational Formulation of the Flow Rule ............. 616
105.8 Plastic Free-Energy Balance .......................... 617
105.9 Some Remarks ......................................... 618
PART XVIII. SINGLE CRYSTALS UNDERGOING LARGE DEFORMATIONS ..... 621
106 Basic Single-Crystal Kinematics ........................... 623
107 The Burgers Vector and the Flow of Screw and Edge
Dislocations ............................................... 626
107.1 Transformation of Vector Area Measures Between the
Reference, Observed, and Lattice Spaces .............. 626
107.2 Characterization of the Burgers Vector ............... 627
107.3 The Plastically Convected Rate of G .................. 629
107.4 Densities of Screw and Edge Dislocations ............. 631
107.5 Comparison of Small- and Large-Deformation Results
Concerning Dislocation Densities ..................... 633
108 Virtual-Power Formulation of the Standard and Microscopic
Force Balances ............................................. 634
108.1 Internal and External Expenditures of Power .......... 634
108.2 Consequences of Frame-Indifference ................... 636
108.3 Macroscopic and Microscopic Force Balances ........... 637
109 Free-Energy Imbalance ..................................... 639
110 Conventional Theory ....................................... 641
110.1 Constitutive Relations ............................... 641
110.2 Simplified Constitutive Theory ....................... 643
110.3 Summary of Basic Equations ........................... 644
111 Taylor's Model of Polycrystal ............................. 646
111.1 Kinematics of a Taylor Polycrystal ................... 646
111.2 Principle of Virtual Power ........................... 648
111.3 Free-Energy Imbalance ................................ 651
111.4 Constitutive Relations ............................... 651
112 Single-Crystal Plasticity at Small Length Scales: A
Large-Deformation Gradient Theory .......................... 653
112.1 Energetic Constitutive Equations. Peach-Koehler
Forces ............................................... 653
112.2 Dissipative Constitutive Equations that Account for
Slip-Rate Gradients .................................. 654
l|2.3 Viscoplastic Flow Rule ............................... 656
112.4 Microscopically Simple Boundary Conditions ........... 657
112.5 Variational Formulation .............................. 658
112.6 Plastic Free-Energy Balance .......................... 659
112.7 Some Remarks ......................................... 660
113 Isotropic Functions ....................................... 665
113.1 Isotropic Scalar Functions ........................... 666
113.2 Isotropic Tensor Functions ........................... 666
113.3 Isotropic Linear Tensor Functions .................... 668
114 The Exponential of a Tensor ............................... 669
References ................................................. 671
Index ...................................................... 683
|