Contributors ................................................... ix
Preface ........................................................ xi
1 Graph Theory for Systems Biology: Interval Graphs,
Motifs, and Pattern Recognition
John R. Jungck and Rama Viswanathan
1.1 Introduction ............................................... 1
1.2 Revisualizing, Recognizing, and Reasoning About
Relationships .............................................. 3
1.2.1 Basic Concepts from Graph Theory .................... 3
1.2.2 Interval Graphs in Biology .......................... 6
1.3 Example I—Differentiation: Gene Expression ................ 15
1.4 Example II—Disease Etiology ............................... 20
1.5 Conclusion ................................................ 25
Acknowledgments ................................................ 26
References ..................................................... 26
2 Food Webs and Graphs
Margaret (Midge) Cozzens
2.1 Introduction .............................................. 29
2.2 Modeling Predator-Prey Relationships with Food Webs ....... 29
2.3 Trophic Levels and Trophic Status ......................... 30
2.3.1 Background and Definitions ......................... 31
2.3.2 Adding Complexity: Weighted Food Webs and Flow-
Based Trophic Levels ............................... 35
2.3.3 Flow-Based Trophic Level ........................... 36
2.4 Competition Graphs and Habitat Dimension .................. 37
2.4.1 Competition Graphs (also Called Niche Overlap
Graphs and Predator Graphs) ........................ 37
2.4.2 Interval Graphs and Bцxicity ....................... 37
2.4.3 Habitat Dimension .................................. 40
2.5 Connectance, Competition Number, and Projection Graphs .... 41
2.5.1 Connectance ........................................ 42
2.5.2 Competition Number ................................. 43
2.5.3 Projection Graphs .................................. 44
2.6 Conclusions ............................................... 48
References ................................................ 49
3 Adaptation and Fitness Graphs
Kristina Crona and Emilie Wiesner
3.1 Introduction .............................................. 51
3.2 Fitness Landscapes and Fitness Graphs ..................... 52
3.2.1 Basic Terminology and Notation ..................... 52
3.2.2 Fitness, Fitness Landscapes, and Fitness Graphs .... 53
3.2.3 Epistasis .......................................... 55
3.3 Fitness Graphs and Recombination .......................... 58
3.4 Fitness Graphs and Drug Cycling ........................... 60
References ................................................ 63
4 Signaling Networks: Asynchronous Boolean Models
Réka Albert and Raina Robeva
4.1 Introduction to Signaling Networks ........................ 65
4.2 A Brief Summary of Graph-Theoretic Analysis of Signaling
Networks .................................................. 66
4.3 Dynamic Modeling of Signaling Networks .................... 69
4.4 The Representation of Node Regulation in Boolean Models ... 70
4.5 The Dynamics of Boolean Models ............................ 72
4.6 Aftractor Analysis for Stochastic Asynchronous Update ..... 75
4.7 Boolean Models Capture Characteristic Dynamic Behavior .... 77
4.8 How to Deal with Incomplete Information when
Constructing the Model .................................... 80
4.8.1 Dealing with Gaps in Network Construction .......... 81
4.8.2 Dealing with Gaps in Transition Functions .......... 82
4.8.3 Dealing with Gaps in Initial Condition ............. 84
4.8.4 Dealing with Gaps in Timing Information ............ 85
4.9 Generate Novel Predictions with the Model ................. 85
4.10 Boolean Rule-Based Structural Analysis of Cellular
Networks .................................................. 86
4.11 Conclusions ............................................... 90
References ................................................ 90
5 Dynamics of Complex Boolean Networks: Canalization,
Stability, and Criticality
Qijun He, Matthew Macauley and Robin Davies
5.1 Introduction .............................................. 93
5.2 Boolean Network Models .................................... 95
5.2.1 Gene Regulatory Networks ........................... 95
5.2.2 Network Topology ................................... 96
5.2.3 Network Topology and Random Networks ............... 99
5.2.4 Boolean Functions ................................. 100
5.2.5 Boolean Networks .................................. 102
5.3 Canalization ............................................. 104
5.3.1 Canalizing Boolean Functions ...................... 104
5.3.2 Nested Canalizing Functions ....................... 105
5.3.3 Canalizing Depth .................................. 109
5.3.4 Dominant Variables of NCFs ........................ 110
5.4 Dynamics Over Complex Networks ........................... 112
5.4.1 Boolean Calculus .................................. 113
5.4.2 Derrida Plots and the Three Dynamical Regimes ..... 115
5.4.3 Ensembles of RBNs ................................. 116
Acknowledgments .......................................... 118
References ............................................... 118
6 Steady State Analysis of Boolean Models: A Dimension
Reduction Approach
Alan Veliz-Cuba and David Murrugarra
6.1 Introduction ............................................. 121
6.2 An Example: Toy Model of the lac Operon .................. 122
6.3 General Reduction ........................................ 125
6.3.1 Definition ........................................ 125
6.3.2 Examples .......................................... 125
6.4 Implementing the Reduction Algorithm Using Boolean
Algebra .................................................. 128
6.5 Implementing the Reduction Algorithm Using Polynomial
Algebra .................................................. 129
6.5.1 Background ........................................ 129
6.5.2 Using Polynomial Algebra Software to Reduce
Boolean Networks .................................. 130
6.6 Applications ............................................. 131
6.6.1 The lac Operon .................................... 131
6.6.2 Th-Cell Differentiation ........................... 133
6.7 AND Boolean Models ....................................... 134
6.7.1 Background ........................................ 135
6.8 Conclusion ............................................... 137
References ............................................... 138
7 BioModel Engineering with Petri Nets
Mary Ann Blätke, Monika Heinerand Wolfgang Marwan
7.1 Introduction ............................................. 141
7.2 Running Case Study ....................................... 144
7.3 Petri Nets (  ) .......................................... 146
7.3.1 Modeling .......................................... 146
7.3.2 Analysis .......................................... 153
7.3.3 Further Reading ................................... 159
7.3.4 Exercises ......................................... 160
7.4 Stochastic Petri Nets ( ) .......................................... 146
7.3.1 Modeling .......................................... 146
7.3.2 Analysis .......................................... 153
7.3.3 Further Reading ................................... 159
7.3.4 Exercises ......................................... 160
7.4 Stochastic Petri Nets (  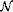 ) .............................. 162
7.4.1 Modeling .......................................... 162
7.4.2 Analysis .......................................... 165
7.4.3 Further Reading ................................... 169
7.4.4 Exercises ......................................... 170
7.5 Continuous Petri Nets (C ) .............................. 162
7.4.1 Modeling .......................................... 162
7.4.2 Analysis .......................................... 165
7.4.3 Further Reading ................................... 169
7.4.4 Exercises ......................................... 170
7.5 Continuous Petri Nets (C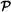 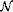 ) .............................. 172
7.5.1 Modeling .......................................... 172
7.5.2 Analysis .......................................... 173
7.5.3 Further Reading ................................... 175
7.5.4 Exercises ......................................... 176
7.6 Hybrid Petri Nets ( ) .............................. 172
7.5.1 Modeling .......................................... 172
7.5.2 Analysis .......................................... 173
7.5.3 Further Reading ................................... 175
7.5.4 Exercises ......................................... 176
7.6 Hybrid Petri Nets (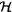 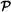 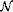 ) .................................. 177
7.6.1 Modeling .......................................... 178
7.6.2 Analysis .......................................... 180
7.6.3 Further Reading ................................... 181
7.6.4 Exercises ......................................... 182
7.7 Colored Petri Nets ....................................... 183
7.7.1 Further Reading ................................... 186
7.7.2 Exercises ......................................... 186
7.8 Conclusions .............................................. 187
Acknowledgments .......................................... 189
7.9 Supplementary Materials .................................. 189
References ............................................... 189
8 Transmission of Infectious Diseases: Data, Models, and
Simulations
Winfried Just, Hannah Callender, M. Drew LaMar and
Natalia Toporikova
8.1 Introduction: Why Do We Want to Model Infectious
Diseases? ................................................ 193
8.2 Mathematical Models of Disease Transmission .............. 198
8.2.1 Transmission Probabilities ........................ 199
8.2.2 The Time Line of Within-Host Dynamics ............. 201
8.2.3 Movement Between Compartments ..................... 203
8.2.4 Basic Model Types: SEIR, SIR, SI, and SIS ......... 206
8.2.5 How to Model Time and Run Simulations ............. 208
8.3 How Does the Computer Run Simulations? ................... 210
8.3.1 Meet the Simulator ................................ 210
8.3.2 How to Load the Die ............................... 212
References ............................................... 214
9 Disease Transmission Dynamics on Networks: Network
Structure Versus Disease Dynamics
Winfried Just, Hannah Callender and M. Drew LaMar
9.1 Introduction ............................................. 217
9.2 Models Based on the Uniform Mixing Assumption ............ 218
9.2.1 Compartment-Based Models .......................... 218
9.2.2 The Basic Reproductive Ratio R0 ................... 220
9.3 Network-Based Models ..................................... 224
9.3.1 Networks and Graphs ............................... 225
9.3.2 Disease Transmission on Networks .................. 229
9.3.3 Examples of Contact Networks ...................... 230
9.3.4 Additional Graph-Theoretic Notions ................ 231
9.3.5 Erdős-Rényi Random Graphs ......................... 233
9.4 Suggestions for Further Study ............................ 234
Acknowledgments .......................................... 235
References ............................................... 235
10 Predicting Correlated Responses in Quantitative Traits
Under Selection: A Linear Algebra Approach
Janet Steven and Bessie Kirkwood
10.1 Introduction ............................................. 237
10.2 Quantifying Selection on Quantitative Traits ............. 238
10.2.1 Describing Traits Mathematically .................. 238
10.2.2 Quantifying Reproduction and Survival ............. 241
10.2.3 Describing the Relationship Between Fitness and
a Trait ........................................... 242
10.2.4 Determining the Genetic Component of Quantitative
Traits ............................................ 245
10.2.5 Estimating Heritability in a Trait ................ 246
10.2.6 The Breeder's Equation ............................ 247
10.2.7 The Price Equation ................................ 249
10.3 Covariance Among Traits Under Selection .................. 249
10.3.1 Nonindependence of Multiple Traits ................ 250
10.3.2 The Genetic Variance-Covariance Matrix ............ 252
10.3.3 Simultaneous Selection on Multiple Traits ......... 253
10.3.4 Predicting the Outcome of Selection on Covarying
Traits ............................................ 255
10.3.5 Evolution of the G Matrix Itself .................. 257
References ............................................... 258
11 Metabolic Analysis: Algebraic and Geometric Methods
Terrell L. Hodge, Blair R. Szymczyna and Todd J. Barkman
11.1 Introduction ............................................. 261
11.2 Encoding the Reactions: Linear Algebraic Modeling ........ 262
11.3 Adding Reaction Kinetics: Algebraic Formulation of
Mass-Action Kinetics ..................................... 271
11.4 Directions for Further Reading and Research: Metabolic
Pathways ................................................. 273
11.5 NMR and Linear Algebraic Methods ......................... 274
11.6 NMR Spectroscopy and Applications to the Study of
Metabolism ............................................... 274
11.6.1 Principles of NMR Spectroscopy .................... 275
11.6.2 The NMR Spectrum .................................. 277
11.6.3 NMR Investigations of Metabolism .................. 281
11.7 NMR for Metabolic Analysis and Mathematical Methods:
Directions of Further Research ........................... 289
11.8 Supplementary Materials .................................. 290
References ............................................... 290
12 Reconstructing the Phylogeny: Computational Methods
Grady Weyenberg and Ruriko Yoshida
12.1 Introduction ............................................. 293
12.1.1 Sequences and Alignments .......................... 297
12.2 Quantifying Evolutionary Change .......................... 299
12.2.1 Probabilistic Models of Molecular Evolution ....... 299
12.2.2 Common Model Extensions ........................... 306
12.3 Reconstructing the Tree .................................. 306
12.3.1 Distance-Based Methods ............................ 306
12.3.2 Maximum Parsimony ................................. 309
12.3.3 Methods Based on Probability Models ............... 310
12.4 Model Selection .......................................... 312
12.5 Statistical Methods to Test Congruency Between Trees ..... 313
References .................................................... 316
13 RNA Secondary Structures: Combinatorial Models and
Folding Algorithms
Qijun He, Matthew Macauley and Robin Davies
13.1 Introduction ............................................. 321
13.2 Combinatorial Models of Noncrossing RNA Structures ....... 324
13.2.1 Partial Matchings and Physical Constraints ........ 324
13.2.2 Loop Decomposition ................................ 327
13.3 Energy-Based Folding Algorithms for Secondary Structure
Prediction ............................................... 329
13.3.1 Maximizing Bond Strengths via Dynamic
Programming ....................................... 329
13.3.2 Minimum Free Energy Folding ....................... 333
13.4 Stochastic Folding Algorithms via Language Theory ........ 335
13.4.1 Languages and Grammars ............................ 335
13.4.2 RNA Secondary Structures .......................... 337
13.4.3 Secondary Structure Prediction Using SCFGs ........ 340
13.4.4 Summary ........................................... 341
13.5 Pseudoknots .............................................. 341
Acknowledgments .......................................... 344
References ............................................... 344
14 RNA Secondary Structures: An Approach Through
Pseudoknots and Fatgraphs
Christian M. Reidys
14.1 Introduction ............................................. 347
14.2 Fatgraphs and Shapes ..................................... 349
14.3 Genus Recursion .......................................... 354
14.4 Shapes of Fixed Topological Genus ........................ 357
Acknowledgments ............................................... 361
References .................................................... 361
Index ......................................................... 363 ) .................................. 177
7.6.1 Modeling .......................................... 178
7.6.2 Analysis .......................................... 180
7.6.3 Further Reading ................................... 181
7.6.4 Exercises ......................................... 182
7.7 Colored Petri Nets ....................................... 183
7.7.1 Further Reading ................................... 186
7.7.2 Exercises ......................................... 186
7.8 Conclusions .............................................. 187
Acknowledgments .......................................... 189
7.9 Supplementary Materials .................................. 189
References ............................................... 189
8 Transmission of Infectious Diseases: Data, Models, and
Simulations
Winfried Just, Hannah Callender, M. Drew LaMar and
Natalia Toporikova
8.1 Introduction: Why Do We Want to Model Infectious
Diseases? ................................................ 193
8.2 Mathematical Models of Disease Transmission .............. 198
8.2.1 Transmission Probabilities ........................ 199
8.2.2 The Time Line of Within-Host Dynamics ............. 201
8.2.3 Movement Between Compartments ..................... 203
8.2.4 Basic Model Types: SEIR, SIR, SI, and SIS ......... 206
8.2.5 How to Model Time and Run Simulations ............. 208
8.3 How Does the Computer Run Simulations? ................... 210
8.3.1 Meet the Simulator ................................ 210
8.3.2 How to Load the Die ............................... 212
References ............................................... 214
9 Disease Transmission Dynamics on Networks: Network
Structure Versus Disease Dynamics
Winfried Just, Hannah Callender and M. Drew LaMar
9.1 Introduction ............................................. 217
9.2 Models Based on the Uniform Mixing Assumption ............ 218
9.2.1 Compartment-Based Models .......................... 218
9.2.2 The Basic Reproductive Ratio R0 ................... 220
9.3 Network-Based Models ..................................... 224
9.3.1 Networks and Graphs ............................... 225
9.3.2 Disease Transmission on Networks .................. 229
9.3.3 Examples of Contact Networks ...................... 230
9.3.4 Additional Graph-Theoretic Notions ................ 231
9.3.5 Erdős-Rényi Random Graphs ......................... 233
9.4 Suggestions for Further Study ............................ 234
Acknowledgments .......................................... 235
References ............................................... 235
10 Predicting Correlated Responses in Quantitative Traits
Under Selection: A Linear Algebra Approach
Janet Steven and Bessie Kirkwood
10.1 Introduction ............................................. 237
10.2 Quantifying Selection on Quantitative Traits ............. 238
10.2.1 Describing Traits Mathematically .................. 238
10.2.2 Quantifying Reproduction and Survival ............. 241
10.2.3 Describing the Relationship Between Fitness and
a Trait ........................................... 242
10.2.4 Determining the Genetic Component of Quantitative
Traits ............................................ 245
10.2.5 Estimating Heritability in a Trait ................ 246
10.2.6 The Breeder's Equation ............................ 247
10.2.7 The Price Equation ................................ 249
10.3 Covariance Among Traits Under Selection .................. 249
10.3.1 Nonindependence of Multiple Traits ................ 250
10.3.2 The Genetic Variance-Covariance Matrix ............ 252
10.3.3 Simultaneous Selection on Multiple Traits ......... 253
10.3.4 Predicting the Outcome of Selection on Covarying
Traits ............................................ 255
10.3.5 Evolution of the G Matrix Itself .................. 257
References ............................................... 258
11 Metabolic Analysis: Algebraic and Geometric Methods
Terrell L. Hodge, Blair R. Szymczyna and Todd J. Barkman
11.1 Introduction ............................................. 261
11.2 Encoding the Reactions: Linear Algebraic Modeling ........ 262
11.3 Adding Reaction Kinetics: Algebraic Formulation of
Mass-Action Kinetics ..................................... 271
11.4 Directions for Further Reading and Research: Metabolic
Pathways ................................................. 273
11.5 NMR and Linear Algebraic Methods ......................... 274
11.6 NMR Spectroscopy and Applications to the Study of
Metabolism ............................................... 274
11.6.1 Principles of NMR Spectroscopy .................... 275
11.6.2 The NMR Spectrum .................................. 277
11.6.3 NMR Investigations of Metabolism .................. 281
11.7 NMR for Metabolic Analysis and Mathematical Methods:
Directions of Further Research ........................... 289
11.8 Supplementary Materials .................................. 290
References ............................................... 290
12 Reconstructing the Phylogeny: Computational Methods
Grady Weyenberg and Ruriko Yoshida
12.1 Introduction ............................................. 293
12.1.1 Sequences and Alignments .......................... 297
12.2 Quantifying Evolutionary Change .......................... 299
12.2.1 Probabilistic Models of Molecular Evolution ....... 299
12.2.2 Common Model Extensions ........................... 306
12.3 Reconstructing the Tree .................................. 306
12.3.1 Distance-Based Methods ............................ 306
12.3.2 Maximum Parsimony ................................. 309
12.3.3 Methods Based on Probability Models ............... 310
12.4 Model Selection .......................................... 312
12.5 Statistical Methods to Test Congruency Between Trees ..... 313
References .................................................... 316
13 RNA Secondary Structures: Combinatorial Models and
Folding Algorithms
Qijun He, Matthew Macauley and Robin Davies
13.1 Introduction ............................................. 321
13.2 Combinatorial Models of Noncrossing RNA Structures ....... 324
13.2.1 Partial Matchings and Physical Constraints ........ 324
13.2.2 Loop Decomposition ................................ 327
13.3 Energy-Based Folding Algorithms for Secondary Structure
Prediction ............................................... 329
13.3.1 Maximizing Bond Strengths via Dynamic
Programming ....................................... 329
13.3.2 Minimum Free Energy Folding ....................... 333
13.4 Stochastic Folding Algorithms via Language Theory ........ 335
13.4.1 Languages and Grammars ............................ 335
13.4.2 RNA Secondary Structures .......................... 337
13.4.3 Secondary Structure Prediction Using SCFGs ........ 340
13.4.4 Summary ........................................... 341
13.5 Pseudoknots .............................................. 341
Acknowledgments .......................................... 344
References ............................................... 344
14 RNA Secondary Structures: An Approach Through
Pseudoknots and Fatgraphs
Christian M. Reidys
14.1 Introduction ............................................. 347
14.2 Fatgraphs and Shapes ..................................... 349
14.3 Genus Recursion .......................................... 354
14.4 Shapes of Fixed Topological Genus ........................ 357
Acknowledgments ............................................... 361
References .................................................... 361
Index ......................................................... 363
|